MENUCours de Thermodynamique

L'étude des machines thermiques, qui historiquement est à l'origine de la naissance de la thermodynamique, est ici présentée comme une conséquence des principes de la thermodynamique. La machine frigorifique et le moteur de Stirling permettront d'illustrer notre propos.

Théorie des machines

Généralités

Une machine thermique est un dispositif qui permet d'effectuer des conversions d'énergie thermique en travail, de travail en énergie thermique et/ou des transferts thermiques d'une source à une autre. Ceci est réalisé grâce à un fluideLe fluide sera notre système thermodynamique. qui subit un cycle de transformations. Le cycle est :

• fermé, s'il n'y'a pas d'échange de matière avec l'extérieur ;
• ouvert dans le cas contraire.

On distingue deux types de machines thermiques :

• les moteurs sont des machines qui fournissent un travail mécanique global vers l'extérieur : \(W<0\) ;
• les récepteurs sont des machines qui reçoivent du travail afin de produire un transfert thermique dans un sens non naturel (du froid vers le chaud).

Pour mesurer la performance de ces conversions d'énergie, on définit l'efficacitéOn parle aussi de facteur de performance. par le facteur \begin{equation} \fcolorbox{#FF9D00}{#FEF5EB}{\quad \(\displaystyle \eta=\left|\frac{\text{énergie utile}}{\text{énergie couteuse}}\right| \)\quad} \;\color{#FF9900}{\heartsuit} \end{equation}

Cycle monoherme fermé

Considérons un fluide échangeant, au cours d'un cycle, une énergie thermique \(Q_1\) avec un thermostatRappelons qu'un thermostat est un système de suffisamment grande capacité thermique pour que tout apport ou retrait d'énergie thermique n'entraîne aucune variation de sa température. de température \(T_1\), et un travail total \(W\). On parle de cycle monotherme.

Les bilans d'énergie et d'entropie effectués sur un cycle nous amène à écrire \[ \Delta U=0=Q_1+W \quad\text{et}\quad \Delta S=0=\frac{Q_1}{T_1}+S_\text{c}\geq \frac{Q_1}{T_1} \] En effet, comme le fluide revient dans le même état après un cycle, la variation de toute fonction d'état est nulle après un cycle. On en tire \(Q_1\leq 0\) et \(W\geq 0\). Autrement dit, ça ne peut pas être un moteur.

Cet énoncé que l'on doit à William Thomson (Lord Kelvin) est complètement équivalent au 2^nd principe.

Moteur ditherme

Considérons un fluide qui, au cours d'un cycle de transformations, échange de l'énergie thermique avec deux thermostats. On note \(Q_\text{f}\) le transfert thermique échangé avec une source froide de température \(T_\text{f}\), et \(Q_\text{c}\) celui échangé avec une source chaude de température \(T_\text{c}>T_\text{f}\). On note \(W\) le travail total échangé au cours d'un cycle.

Un bilan d'énergie et d'entropie donne : \[ W+Q_\text{f}+Q_\text{c}=0 \quad\text{et}\quad \frac{Q_\text{c}}{T_\text{c}}+\frac{Q_\text{f}}{T_\text{f}}\leq 0 \] Par définition d'un moteur, la machine doit fournir du travail : \(W<0\). Il en découle deux relations d'ordre : \[ Q_\text{c}+Q_\text{f}>0 \quad\text{et}\quad \frac{Q_\text{f}}{T_\text{f}}\leq -\frac{Q_\text{c}}{T_\text{c}} \] c'est-à-dire \[ 0<Q_\text{c}+Q_\text{f}\leq Q_\text{c}\left(1-\frac{T_\text{f}}{T_\text{c}}\right) \] En conclusion, la source chaude doit fournir de la chaleur \((Q_\text{c}>0)\) et la source froide en absorber \((Q_\text{f}<0).\)

Le plus souvent, la source froide est l'atmosphère dont l'existence ne nous coûte rien. L'efficacité du moteur est alors définie par \begin{equation} \fcolorbox{#FF9D00}{#FEF5EB}{\quad \(\displaystyle \eta_\text{moteur}=\frac{|W|}{Q_\text{c}}=\frac{-W}{Q_\text{c}} \)\quad} \;\color{#FF9900}{\heartsuit} \end{equation} Ce rendement ne peut pas dépasser une valeur maximale fixée par la température des sources chaudes et froides. En effet, \[ \frac{-W}{Q_\text{c}}= \frac{Q_\text{c}+Q_\text{f}}{Q_\text{c}}\leq 1-\frac{T_\text{f}}{T_\text{c}}<1 \]

Plus les irréversibilités sont importantes et plus l'efficacité s'éloigne du rendement de Carnot.

Cycle de Carnot — le cycle décrit par un moteur ditherme réversible est dit cycle de Carnot. Il est constitué de deux isothermes \(T_\text{c}\) et \(T_\text{f}\) durant lesquels le fluide échange de l'énergie thermique, et deux adiabatiques réversible, c'est-à-dire deux isentropiques.

Dans le diagramme de Watt (diagramme p-V), le cycle décrit un circuit dont l'aire représente le travail fourni durant un cycle. Ce cycle est décrit dans le sens horaire car \[ \oint_\text{cycle}p \mathrm{d}V=-W>0 \] Dans le diagramme T-S, le cycle de Carnot décrit un rectangle dont l'aire représente la chaleur totale échangée. Ce cycle est décrit dans le sens horaire également car \[ \oint_\text{cycle}T \,\mathrm{d}S=Q_\text{c}+Q_\text{f}>0 \]

Récepteur ditherme

On a les mêmes équations que pour un moteur ditherme à ceci près que \(W>0\) par hypothèse. On distingue deux types de récepteur :

• la machine frigorifique dont le rôle consiste à refroidir une source froide \((Q_\text{f}>0)\) ;
• la pompe à chaleur dont le rôle consiste à réchauffer une source chaude \((Q_\text{c}<0)\).

Machine frigorifique ditherme — Le fluide échange de la chaleur avec une source froide (le local à réfrigérer) et une source chaude (l'extérieur). Le bilan d'énergie et d'entropie donne \[ Q_\text{f}+Q_\text{c}=-W<0 \quad\text{et}\quad \frac{Q_\text{c}}{T_\text{c}}+\frac{Q_\text{f}}{T_\text{f}}\leq 0 \] Par définition \(Q_\text{f}>0\) (la source froide donne de l'énergie au fluide). Par conséquent \(Q_\text{c}<0\) : le fluide cède de l'énergie thermique à l'extérieurOn peut noter que la source chaude reçoit plus de chaleur qu'on en extrait de la source froide, car \(Q_\text{f}+Q_\text{c}<0\)..

L'efficacitéOn parle aussi de COP pour coefficient de performance. d'une machine frigorifique est définie par \begin{equation} \fcolorbox{#FF9D00}{#FEF5EB}{\quad \(\displaystyle \eta_\text{frigo}=\frac{Q_\text{f}}{W} \)\quad} \;\color{#FF9900}{\heartsuit} \end{equation} À l'instar du moteur ditherme, l'efficacité d'une machine frigorifique est maximale lorsque le cycle est décrit de manière réversibleIl s'agit du cycle de Carnot déjà décrit pour le moteur ditherme, à ceci près que le sens de parcours est anti-horaire car \(\oint p\,\mathrm{d}V<0\)., et sa valeur ne dépend que des températures \(T_\text{c}\) et \(T_\text{f}\): \[ \eta^\text{max}_\text{frigo}=\frac{Q_\text{f}}{-Q_\text{f}-Q_\text{c}}= \frac{1}{-Q_\text{c}/Q_\text{f}-1}= \frac{1}{T_\text{c}/T_\text{f}-1}= \frac{T_\text{f}}{\Delta T} \]

Pompe à chaleur ditherme — Récepteur ditherme dont la source chaude correspond au local à chauffer. Par définition \(Q_\text{c}<0\) (la source chaude reçoit de l'énergie de la part du fluide). Les principes de la thermodynamique aboutissent aux même conclusions que pour la machine frigorifique. Cependant, la définition de l'efficacité est différente : \begin{equation} \fcolorbox{#FF9D00}{#FEF5EB}{\quad \(\displaystyle \eta_\text{PAC}=\frac{|Q_\text{c}|}{W} \)\quad} \;\color{#FF9900}{\heartsuit} \end{equation} Là encore le facteur de performance est maximum lorsque les transformations sont réversibles. On laisse le lecteur vérifier que \[ \eta^\text{max}_\text{PAC}=\frac{T_\text{c}}{\Delta T} \]

Étude d'une machine frigorifique

Les changements d'état sont mis à profit dans les machines frigorifiques et les pompes à chaleur. L'utilisation d'un mélange liquide/gaz est particulièrement intéressante dans la mesure où l'évaporation ou la liquéfaction peuvent s'effecteur à température constante, ce qui permet d'obtenir des efficacités proches de l'efficacité maximale.

Nous détaillons ici le cycle simplifié d'une machine frigorifique.

Principe

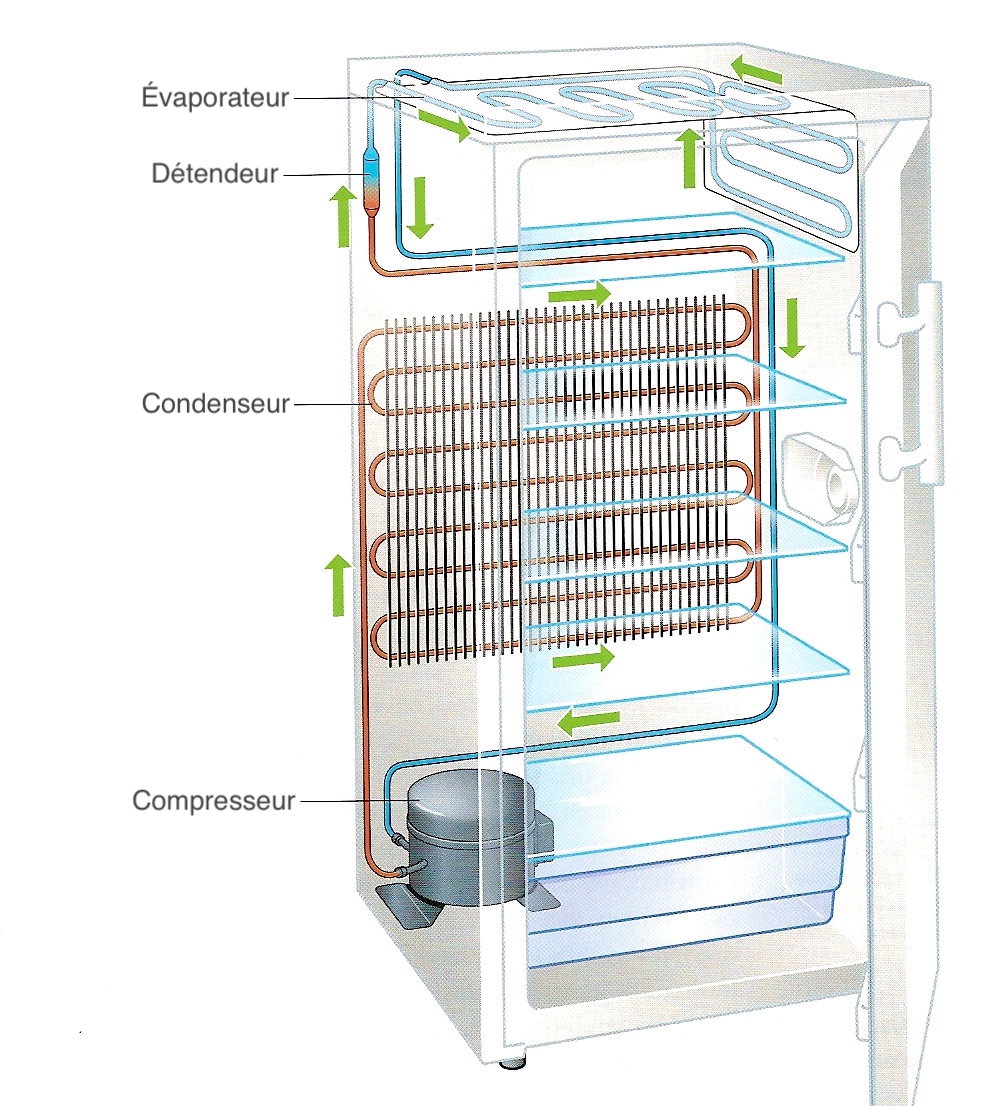
Un fluide (ammoniac, isobutane, fréons, ...) décrit un cycle au cours duquel il change d'état. Lors de la vaporisation dans l'évaporateur, le fluide absorbe de l'énergie thermique provenant du local à réfrigérer, ce qui permet de le maintenir froid. Décrivons le cycle thermodynamique décrit par le fluide (Fig.7).

• Transformation AB : le fluide à l'état de vapeur sèche passe dans un compresseur qui augmente la pression du fluide. Cette compression peut être assimilée en première approximation à une compression adiabatique réversible. La température augmente donc.
• Transformation BC : la vapeur sèche passe dans le condenseur et cède de la chaleur à l'extérieur en se liquéfiant (\(Q_\text{BC}\)). Supposons que C se trouve sur la courbe de saturation (courbe d'ébullition).
• Transformation CD : le liquide passe à travers un détendeur. On assimilera cette détente à une détente de Joule-Thomson qui conserve l'enthalpie. Cette détente produit une vaporisation partielle et un refroidissement.
• Transformation DA : enfin, le mélange liquide/vapeur s'enrichit en vapeur dans l'évaporateur jusqu'à atteindre l'état de vapeur sèche, ce qui absorbe la quantité d'énergie thermique \(Q_\text{DA}\). Le cycle se répète ensuite.

Calcul de l'efficacité

Décrivons le cycle dans un diagramme p-v en échelle log, et dans un diagramme des frigoristes (Fig.8). Le trajet AB est supposé adiabatique réversible. Si le fluide est un gaz parfait, la loi de Laplace nous indique que le trajet AB est rectiligne de pente \(-\gamma\). En B on a de la vapeur sèche chaude. Le passage dans le condenseur, le refroidit à la température \(T_\text{c}\) puis le liquéfie entièrement. Le passage dans le détendeur de Joule-Thomson conserve l'enthalpie : le trajet est donc vertical dans le diagramme des frigoristes. On arrive sur un palier de température \(T_\text{f}\). Il est possible de connaître la composition du mélange à partir de la règle des moments. Enfin, le trajet DA referme le cycle en vaporisant complètement le liquide ce qui absorbe un énergie thermique \(Q_\text{f}\).

L'efficacité vaut, si les phases AB et CD sont adiabatiques : \[ \eta=\frac{Q_\text{DA}}{W}=\frac{Q_\text{DA}}{-Q_\text{DA}-Q_\text{BC}} \] ce qui donne en termes d'enthalpie : \[ \eta=\frac{h_\text{A}-h_\text{D}}{h_\text{D}-h_\text{A}-h_\text{C}+h_\text{B}} \] Ainsi, l'efficacité d'une machine frigorifique se calcule aisément à l'aide d'un diagramme des frigoristes.

On peut aussi la calculer à partir des chaleurs latentes et du titre massique \(x_\text{g}\) de vapeur en sortie du détendeur (point D). En effet, on a \[ \left\{\begin{array}{rcl} h_\text{A}-h_\text{D}&=&m_\ell\ell_\text{vap}(T_\text{f})=m(1-x_\text{g})\ell_\text{vap}(T_\text{f})\\ h_\text{C}-h_\text{B}&=&mc_{p,\text{g}}(T_\text{c}-T_\text{B})+m\ell_\text{liq}(T_\text{c})\\ \end{array}\right. \] On en déduit, en utilisant \(\ell_\text{liq}(T_\text{c})=-\ell_\text{vap}(T_\text{c})\), \[ \eta= \frac{(1-x_\text{g})\ell_\text{vap}(T_\text{f})}{\ell_\text{vap}(T_\text{c})-(1-x_\text{g})\ell_\text{vap}(T_\text{f})+c_{p,\text{g}}(T_\text{B}-T_\text{c})} \]

Le moteur de Stirling

Description

En 1816, il y a plus de deux siècles, l'ingénieur Robert Stirling déposa un brevet décrivant le principe d'un moteur à air chaud. De l'air enfermée dans une enceinte subit différentes compressions et détentes à différentes températures. L'apport de chaleur n'est pas internecontrairement aux moteurs à combustion interne, où c'est la combustion d'un carburant au sein du fluide qui produit un transfert thermique., mais externe, et peut être d'origine chimique (combustion), solaire et même nucléaire.

Ce type de moteur fait l'objet de nombreuses recherches, et il n'est pas impossible que dans un futur proche ce moteur joue un rôle dans la production d'électricité à usage local, du fait de ses nombreux avantages :

• il présente un bon rendement ;
• il est silencieux du fait de l'absence de valves et de soupapes ;
• sa maintenance est assez simple.

Différentes configurations existent. Décrivons le moteur de Stirling dans une configuration dite \(\gamma\).

De l'air est enfermé dans une enceinte hermétique et subit différentes transformations grâce à l'emploi de deux pistons qui exécutent des mouvements déphasés de 90°.

• Le piston moteur (PM) actionne un volant d'inertie lequel est relié, via une courroie, à un générateur électrique ce qui permet une conversion d'énergie mécanique en énergie électrique.
• Le piston de refoulement (PR) permet juste de déplacer l'air en la mettant en contact avec la source chaude ou en l'éloignant de celle-ci.

L'air subit un cycle qui peut se décomposer en 4 phases :

1. PR en bas. L'air est chauffé par la source chaude, ce qui provoque son expansion, et ce qui pousse le piston moteur vers le bas. Ainsi, le compartiment froid voit arriver de l'air chaud. Cette dilatation de l'air se fait quasiment à température constante.
2. PM en bas. Le mouvement de la roue entraîne le piston de refoulement vers le haut. Ici le volume ne varie pas, mais l'air chaud étant déplacé vers le bas, il y a refroidissement.
3. PR en haut. Le piston moteur remonte, aidé par la baisse de pression. L'air subit une compression quasi isotherme.
4. PM en haut. Le piston de refoulement descend ce qui amène de l'air froid dans le compartiment chauffé par la source chaude. La pression augmente de façon isochore.

Ce cycle est dit régénératif car un régénérateur permet de stocker de la chaleur lors du passage du gaz chaud dans le compartiment froid (phase 2), puis de la restituer au gaz froid lors de la phase 4. C'est cette invention que l'on doit à Robert Stirling et qui rend son moteur efficace.

Calcul du rendement

Calculons le rendement du moteur en se basant sur le cycle idéalisé décrit ci-dessus et en assimilant l'air à un gaz parfait d'exposant adiabatique \(\gamma=1{,}4\). On considèrera que le cycle est décrit de façon quasi statique.

Dans un premier temps, oublions le rôle joué par le régénérateur. Par définition, le rendement s'écrit \[ \eta=\frac{|W|}{Q_\text{reçu}}=\frac{-W}{Q_1+Q_4} \] Le travail mécanique reçu par le fluide vaut \begin{equation} \begin{split} W = - \oint p\,\mathrm{d}V=-\int_{(1)}p\, \mathrm{d}V-\int_{(3)}p\, \mathrm{d}V\\ =-nRT_\text{c}\int_{V_\text{min}}^{V_\text{max}}\frac{\mathrm{d}V}{V} -nRT_\text{f}\int_{V_\text{max}}^{V_\text{min}}\frac{\mathrm{d}V}{V}\nonumber \end{split} \end{equation} Après intégration, on obtient \[ |W|=nR(T_\text{c}-T_\text{f})\ln\left(\frac{V_\text{max}}{V_\text{min}}\right) \] Utilisons maintenant le premier principe pour déterminer les transferts thermiques \(Q_1\) et \(Q_4\). \[ Q_1=\Delta U_1-W_1 \quad\text{et}\quad Q_4=\Delta U_4-W_4 \] \(\Delta U_1\) est nul car la température reste constante. \(W_4\) est également nul car le volume est constant. Finalement, \[ Q_1+Q_4=-W_1+\Delta U_4= nRT_\text{c}\ln\left(\frac{V_\text{max}}{V_\text{min}}\right)+\frac{nR}{\gamma-1}\Delta T \] Finalement, on obtient \[ \eta=\frac{\Delta T \ln(V_\text{max}/V_\text{min})}{T_\text{c}\ln\left(\frac{V_\text{max}}{V_\text{min}}\right)+\frac{\Delta T}{\gamma-1}} \]

En réalité, le rendement théorique est meilleur car on a oublié de tenir compte du rôle du régénérateur. En effet, si l'on considère ce régénérateur parfait, toute la chaleur perdue dans la phase (2) est récupérée durant la phase la phase (4) de sorte que la chaleur \(Q_4\) ne nous coûte rien en réalité. Dans ce contexte, le rendement vaut \[ \eta_{R}=\frac{|W|}{Q_1}=\frac{T_\text{c}-T_\text{f}}{T_\text{c}} \] Autrement dit, le rendement du moteur de Stirling est égal au rendement de Carnot.