MENUSimuler pour apprendre

De quoi s'agit-il ?

En 1925, Ernst Ising propose un modèle simple de physique statistique dans le but de décrire la transition paramagnétique-ferromagnétique. Il faut savoir que certains corps ont la particularité d'acquérir une aimantation spontanée sans qu'il y ait besoin de les soumettre à un champ magnétique (c'est le principe des aimants). Cependant, dès que la température dépasse un seuil que l'on appelle température critique (ou température de CurieEn hommage à Pierre Curie qui, en 1894, étudia expérimentalement l'évolution de la susceptibilité magnétique des corps magnétiques dans leur phase paramagnétique.), ces matériaux perdent leur aimantation.

Dans le modèle d'Ising, \(N\) atomes portant un spin \(\sigma_i\) (et donc un moment magnétique) sont placés sur un réseau régulier. On simplifie en n'autorisant que deux états de spins (\(\sigma_{i}=\pm 1\) correspondant aux états ↑ et ↓). Par ailleurs, il existe une interaction entre deux spins \(\sigma_i\) et \(\sigma_j\) décrite par l'énergie d'interaction \[E_{ij}=-J_{ij}\;\sigma_i\sigma_j\] où \(J_{ij} ≥ 0\) désigne une constante de couplage. Notez que l'énergie est minimale quand les spins \(\sigma_i\) et \(\sigma_j\) sont identiques de sorte que l'état fondamental correspond à un ensemble de spins alignés dans le même sens et donc à une aimantation maximale : on parle de couplage ferromagnétique. Soumis à une faible agitation thermique, cet ordre magnétique peut localement être perturbés sans pour autant que l'effet coopératif entre les spins disparaisse. En revanche, il existe une température critique au dessus de laquelle cet effet coopératif est détruit : l'aimantation moyenne devient nulle. Si le milieu est macroscopique, ce changement de comportement est brutal ; on parle de transition de phasePlus précisément, il s'agit d'une transition de phase du second ordre pour laquelle l'aimantation, l'entropie, l'énergie varient sans connaître de discontinuité. En revanche, la capacité thermique et la susceptibilité magnétique présentent des divergences à la température critique..

Simulations

Méthode

On simule le comportement d'un modèle d'Ising sur un réseau carré avec interaction entre plus proches voisinsSur un réseau carré, les plus proches voisins d'un atome sont au nombre de quatre.. Autrement dit \(J_{ij}=J\) si les atomes \(i\) et \(j\) sont voisins, sinon \(J_{ij}=0\). L'énergie du système vaut \[E=-\frac{1}{2}\sum_{⟨ij⟩} J\,\sigma_i\,\sigma_j\] où la somme concerne seulement les paires \(i-j\) voisins et le facteur 1/2 compense le double comptage. L'aimantation \(M\) étant proportionnelle à la somme des spins, on pose, par souci de simplicité, \[M=\frac{1}{N} \sum_{i=1}^{N}\sigma_i\] La simulation repose sur l'algorithme de Métropolis qui permet d'obtenir des configurations qui obéissent à la statistique de Boltzmann. On accède aux propriétés thermodynamiques en calculant, pour différentes températures, l'aimantation moyenne, l'énergie interne, la susceptibilité magnétique et la capacité thermique. Ces deux dernières grandeurs s'obtiennent à partir du théorème de fluctuation-dissipation : \[\chi_m=\frac{⟨M^2⟩-⟨M⟩^2}{k_BT} \quad\text{et}\quad C_v=\frac{⟨E^2⟩-⟨E⟩^2}{(k_BT)^2}\]

Les effets de bord

Les spins situés à la frontière du réseau n'ont, au maximum, que trois voisins, au lieu de quatre pour ceux situés à l'intérieur du réseau. Pour \(N\) faible, la proportion de ces spins n'est pas toujours négligeable ce qui produit des écarts aux lois thermodynamiques liées aux effets de bords. Une façon de limiter ces effets consiste à imposer des conditions aux limites périodiques dites conditions de Born Von Karman. Tout se passe alors comme si les frontières étaient raccordées de façon à ce que \[\sigma(L+a,y)=\sigma(a,y) \quad\;\quad \sigma(x,L+a)=\sigma(x,a)\] où \(\sigma(x,y)\) désigne le spin situé en \((x,y)\) sur un réseau d'arête \(a\) et de longueur \(L\).

Dernière petite précision : le système d'unités est telle que \(J=1\) et \(k_B=1\). Autrement dit, la température est exprimée en unité de \(J/k_B\).

Observations

Commencez par observer la structure magnétique du réseau à haute température puis abaissez progressivement la température. Attention, à l'approche du point critique, un phénomène de ralentissement critique se produit de sorte que le temps de décorrélation choisi devient insuffisant pour décorréler les échantillons ce qui nécessite d'attendre un certain temps avant que les moyennes se stabilisent. Notez :

• à haute température, l'aimantation est proche de zéro et les fluctuations magnétiques sont de petite taille ;
• à basse température, \(M\) est proche de un et les fluctuations magnétiques sont également de petit taille ;
• au voisinage de la température critique, les fluctuations sont plus importantes et la taille caractéristiques de ces fluctuations se rapproche de la taille du réseauDans la limite thermodynamique, la longueur de corrélation qui mesure la taille typique de ces fluctuations, diverge au point critique.. En conséquence, la susceptibilité et la capacité thermique atteignent leur maximum à la température critique.

Quelques résultats

Voici quelques résultats obtenus sur un réseau de 80x80 spins. Partant de la température \(T=3,5\), on collecte 100 échantillons pour effectuer les moyennes puis l'on abaisse progressivement la température de 0,05 en 0,05. Pour obtenir des échantillons indépendants sur le plan statistique il est nécessaire d'effectuer un grand nombre d'itérations entre chaque mesures : on a choisit un temps de décorrélation de un million d'itérations.

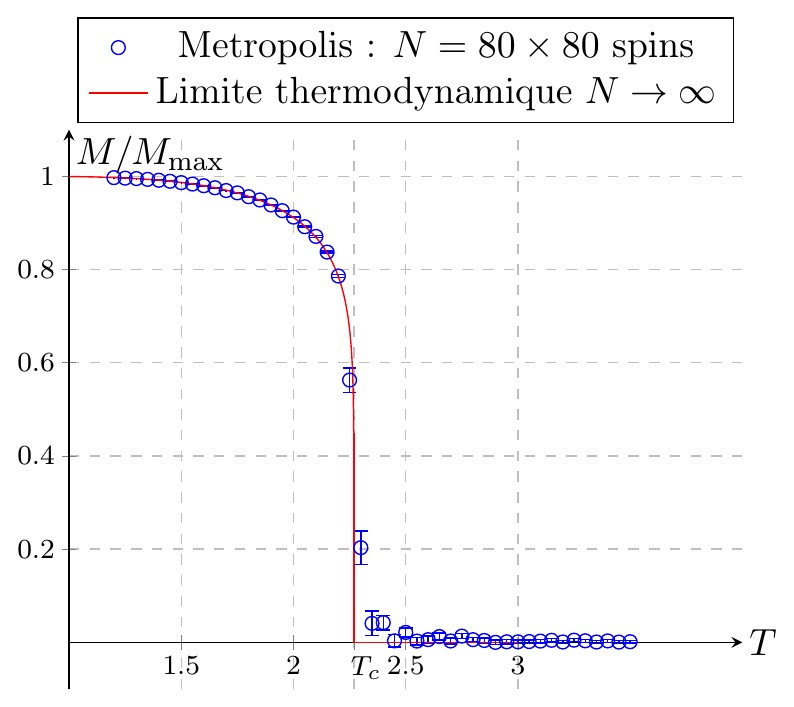
La courbe ci-dessous illustre la chute brutale de l'aimantation autour de \(T=2,3\).

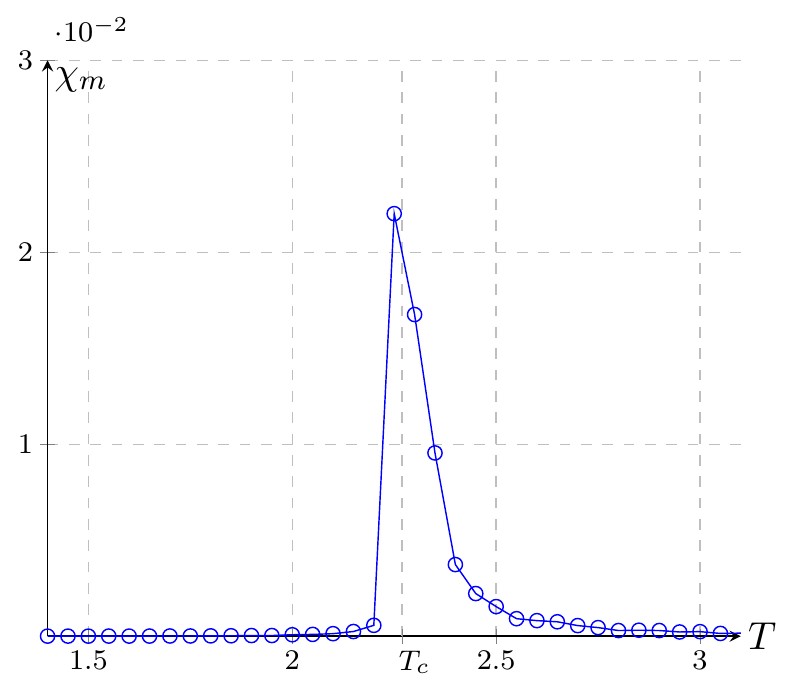
Dans la limite thermodynamique, la susceptibilité magnétique tend vers l'infini à la transition critique. Pour un système fini, elle passe par un maximum. La figure ci-dessous montre un tel comportement avec un maximum autour de \(T=2,25\)

La solution analytique au modèle d'Ising dans la limite thermodynamique a été fournie par Lars Onsager en 1944. \[⟨M⟩(T)= \left\{ \begin{array}{lr} M_{\rm max}\left(1-\frac{1}{\sinh^4(2/T)}\right)^{1/8} & \textrm{pour }T<T_c\\ 0 & \textrm{pour }T>T_c \end{array} \right.\] ce qui montre que l'aimantation moyenne chute brutalement vers la valeur \(⟨M⟩=0\) à une température critique donnée par \[\sinh{\frac{2}{T_c}}=1 \quad\Longrightarrow\quad T_c\simeq 2,269\]